| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Python Hello World
- 파이썬 곱셈
- 백준 1000
- 백준
- 백준 10869
- 백준 1008
- python
- Python 세 자리 곱셈
- 백준 2588
- 백준 사칙연산
- 파이썬 세 자리 곱셈
- 백준 2309
- Python 평균
- Python 나머지
- Hello World
- 파이썬
- 백준 Python
- 백준 1001
- 백준 10998
- Python 곱셈
- 파이썬 나머지
- 파이썬 평균
- 백준 2309 파이썬
- 백준 10430
- 백준 3046
- 백준 일곱 난쟁이
- Python 사칙연산
- 백준 파이썬
- 백준 2557
- Today
- Total
코드 발전소
[백준 문제집][Python 배우기 (101~150)][2309] 일곱 난쟁이 본문
이 글에서 살펴볼 문제는 백준 2309번입니다.
주소는 아래와 같습니다.
https://www.acmicpc.net/problem/2309
2309번: 일곱 난쟁이
아홉 개의 줄에 걸쳐 난쟁이들의 키가 주어진다. 주어지는 키는 100을 넘지 않는 자연수이며, 아홉 난쟁이의 키는 모두 다르며, 가능한 정답이 여러 가지인 경우에는 아무거나 출력한다.
www.acmicpc.net
automata님의 문제집, "Python 배우기 (101~150)"의 20번 문제입니다.
1. 문제 이해
해당 문제는 다음과 같습니다.

간단하게 문제를 살펴봅시다.
굳이 요약하자면, "진짜 난쟁이 7명의 키의 합을 이용해, 가짜 난쟁이 2명을 골라내는 문제"입니다.
문제의 시간 제한, 메모리 제한은 다음과 같습니다.

문제의 입력과 출력 조건은 다음과 같습니다.

문제에서 제시된 예제 입출력은 다음과 같습니다.


2. 어떻게 해결할 것인가?
처음 문제를 보면 막막할 수 있습니다.
그도 그럴 것이, 일곱 난쟁이의 키의 합이 100이 된다는 점을 이용해 문제를 풀어야 하는 상황이므로,
무작위로 주어진 아홉 난쟁이의 키들 중 일곱 난쟁이를 선택하여
그 키의 합이 정확히 100이 되어야 하는 상황이기 때문이죠.
그러나, 이렇게 한 번 생각해 볼 수 있지 않을까요?
오히려 일곱 난쟁이의 키의 합이 100인 것을 이용해서
반대로 나머지 가짜 난쟁이 키의 합을 구할 수 있지 않을것이냐는 겁니다.
즉, 이런 방정식을 세울 수 있지 않을까요?

어떠신가요. 감이 좀 오셨나요?
그러나 갑자기 이런 생각이 당연히 드실 수도 있습니다.
"코드나 알고리즘을 작성할 때
그냥 일곱 난쟁이의 키의 합이 100인 것을 그대로 이용해서
작성해도 괜찮지 않을까?"
네. 당연히 괜찮습니다.
잠시 이야기가 옆으로 새겠지만, 수학적으로 위의 생각이 괜찮은지 같이 분석해봅시다.
만약 독자분들이 고등학교 교육과정의 확률을 배우셨다면,
조합(Combination)을 배우셨을 겁니다.
이 개념을 이용해 간단하게 한 번 분석해봅시다.
아직 조합에 대해 배우지 않으신 분들이라면,
아래에 위키백과의 주소를 첨부해드릴테니,
간단하게 읽고 오셔도 좋고, 2 - 1. 을 건너 뛰셔도 괜찮습니다!
https://ko.wikipedia.org/wiki/%EC%A1%B0%ED%95%A9
조합 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 조합론에서, 조합(組合, 문화어: 무이, 영어: combination)은 집합에서 일부 원소를 취해 부분집합을 만드는 방법을 말한다. 그 경우의 수는 이항계수이다. n개의 원소의 k-조합[편집] n {\displaystyle n} 개의 원소를 가지는 집합에서 k {\displaystyle k} 개의 부분집합을 고르는 조합의 경우의 수를 이항계수라 하며, n C k {\displaystyle _{n}C_{k}\;} 나 n
ko.wikipedia.org
2 - 1. 괜찮지 않을까??
우선, 아홉 명의 난쟁이들 중 순서를 고려하지 않고, 두 명의 난쟁이들을 고르는 경우의 수에 대해 살펴봅시다.
(아홉 명의 난쟁이들은 모두 다르다고 가정합시다.)

위 처럼 난쟁이 아홉 명이 있다고 가정합시다.
두 명의 난쟁이들을 고르기 위해, 우선 1명의 난쟁이를 아무나 골라봅시다.
이 1명의 난쟁이를 고르는 경우의 수는 몇 가지 인지 생각해보면,
당연히 9가지 입니다.
난쟁이들은 모두 다르다고 가정했기 때문에, 서로 다른 난쟁이를 고르는 경우의 수는 총 9가지입니다.
자, 그렇다면 난쟁이를 무작위로 한 명 골랐다 가정하고,
현재 상황을 다시 그림으로 나타내보겠습니다.

이제 남은 난쟁이는 8명입니다.
다시, 8명의 난쟁이 중에서 한 명을 더 골라봅시다.
위와 마찬가지 방법으로, 한 명을 더 고르는 경우의 수는 당연히 8가지 입니다.
다시, 8명의 난쟁이 중 한 명을 무작위로 골랐다 가정합시다.
이제 상황은 아래와 같겠죠.

자, 이렇게 난쟁이 두 명이 골라졌습니다.
총 경우의 수는 몇 가지 인지 계산해봅시다.
"9 X 8 = 72"
총 경우의 수를 72가지라고 계산할 수 있습니다.
그러나, 이 계산 과정에서는 한 가지 간과한 사실이 있습니다.
위 그림처럼, 선택1과 선택2가 존재한다는 사실입니다.
즉, 선택1과 선택2가 존재하는 시점에서 가정하지 않았던 순서가 생겨버린 겁니다.
따라서, 선택1과 선택2의 '자리가 바뀔 수 있다'는 경우의 수를 구해주고,
72에서 이 경우의 수를 나누어 주어야만 저희가 구하는 경우의 수가 나오게 되는 겁니다.
선택1과 선택2의 자리가 바뀔 수 있는 경우의 수는 2가지겠죠.
따라서, 저희가 구하는 진짜 경우의 수는,
"72 / 2 = 36"
36가지입니다.
지금까지 이 이야기를 왜 했냐고 하실 수 있습니다.
이 이야기를 한 이유는 조합(Combination)에 대해 아시는 분들이라면 아시겠지만,
이 이야기 자체를 공식화 시킨 것이 조합(Combination)이기 때문입니다.
그럼 한 번 조합(Combination)을 사용해보겠습니다.
우선,
"코드나 알고리즘을 작성할 때
그냥 일곱 난쟁이의 키의 합이 100인 것을 그대로 이용해서
작성해도 괜찮지 않을까?"
이 생각을 코드상에 옮긴다는 것은, 9명의 난쟁이에서 7명의 난쟁이를 고른다는 생각입니다.
이를 조합(Combination)을 이용해 경우의 수를 찾아보면,
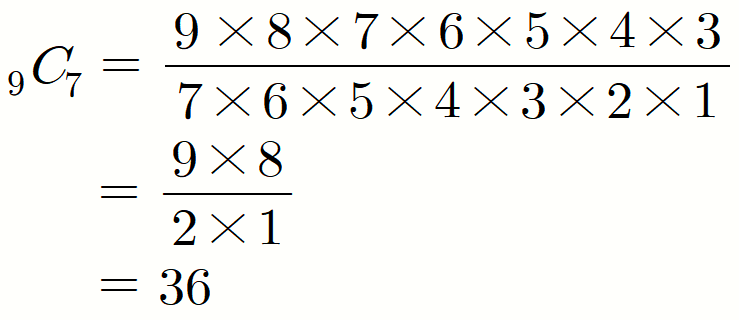
36가지임을 간단하게 알 수 있습니다.
그러나, 조합(Combination)의 성질에 의해,

임을 알 수 있습니다.
따라서 이를 해석하면,
9명의 난쟁이에서 7명의 난쟁이를 고르는 경우의 수나,
9명의 난쟁이에서 2명의 난쟁이를 고르는 경우의 수는 같다는 것입니다.
즉, "정말 최악의 경우"에서는 탐색해야 할 경우의 수가 같다는 소리입니다.
여기까지는 직관적으로 보았을 때의 측면입니다.
그러나, 코드를 짜는 입장에서 다음 질문들을 생각해보십시오.
1. 과연 반복문을 얼마나 중첩시켜야 7명의 난쟁이를 모두 다른 경우로 선택할 수 있을까요?
잘 가늠이 되시나요?
일단 제가 생각나는건 for문을 7중으로 중첩시킨 것 입니다.
그리고 코드를 구체적으로 어떻게 짜야하는 지도 머리속에 곧바로 떠오르지 않습니다.
2. 가독성은 어떨까요?
제가 문제를 풀기 위함 뿐만이 아니라 무언가를 만들기 위해 코드를 짤 때,
가장 중요시 여기는 것은 코드의 가독성입니다.
그 다음이 코드의 효율성이죠.
물론, 문제를 해결할 때는 효율성을 1순위로, 가독성을 2순위로 두는 것이 바람직할 수 있습니다만,
앞서 "정말 최악의 경우"에서는 탐색해야 할 경우의 수가 같다는 것을 수학적으로 보았습니다.
따라서 1순위가 아닌 2순위를 비교해보아야 합니다.
만일, 1번 질문에서 코드를 구체적으로 어떻게 짜야하는 지 머리속에 떠오르지 않으시는 분들은
간단한 코드라도 스파게티처럼 꼬일 수 있게 됩니다.
즉, 코드를 작성함에 있어서 머리속에 코드의 전체적인 흐름이 들어가 있는 것이 아니라,
현재 줄, 현재 작성중인 코드가 포함된 지역의 흐름만 이해하고 있을 수 있다는 겁니다.
그렇게 되면 자연스럽게 코드의 가독성이 떨어지게 됩니다.
결론은,
9명의 난쟁이에서 2명의 난쟁이를 고르는 상황으로 해석하는 것이
코드를, 알고리즘을 작성하는 상황에 있어서 주관적으로는 효율적이라고 생각합니다.
따라서, 코드 및 알고리즘 작성은 2명의 난쟁이를 고른다고 가정하고 진행하도록 하겠습니다.
2 - 2. 알고리즘과 코드의 대략적 구성
가장 먼저 입력 부분을 보겠습니다.
입력은 아홉 난쟁이들의 키를 각각 다른 줄에서 입력받습니다.
for문을 이용해서 모든 난쟁이의 키를 받아봅시다.
모든 난쟁이의 키를 아홉 개의 변수를 만들어 저장하긴 불편할 수 있으니,
난쟁이들의 키를 저장하는 리스트를 만들어서 저장하겠습니다.
또한, 입력을 받을 때, 시간적 효율성을 위해
input() 함수가 아닌, sys 라이브러리의 sys.stdin.readline() 함수를 이용하겠습니다.
다음은 대략적인 알고리즘입니다.
입력을 하고 난 뒤를 예로 들자면,
[10, 20, 30, 40, 50, 60, 70, 80, 90]
와 비슷한 형태의 난쟁이들의 키를 저장하는 리스트가 생겼을 겁니다.
저희가 코드 전체에서 주목해야 할 것은,

위의 방정식입니다.
위 방정식을 기준으로 9명의 난쟁이들 중, 가짜 난쟁이들을 판별해낼 것이기 때문입니다.
따라서, 위에서 만들어낸 난쟁이들의 키를 저장하는 리스트의 원소의 총합을 구해주어 하나의 변수에 저장해줍니다.
그 뒤에는 for문을 이용한 2명의 난쟁이 탐색을 진행해야 합니다.
이 탐색은 2중 for문을 이용해 구성하면 간단하게 구현할 수 있습니다.
2중 for문인 이유는 최악의 경우에 탐색해야 할 경우의 수가,
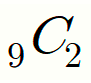
즉, "36가지 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8" 이기 때문입니다.
그림으로 설명을 드리자면,



와 같은 방식으로 탐색을 진행하기 때문입니다.
즉, 파란색으로 둘러친 난쟁이가 바깥쪽 for문에 의해 옮겨지는 난쟁이이고,
노란색으로 둘러친 난쟁이들이 안쪽 for문에 의해 탐색되는 난쟁이입니다.
또한, 노란색으로 둘러친 난쟁이들의 수를 세보면,
8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36임을 알 수 있습니다.
이렇게 2중 for문을 진행하는 도중,
파란색으로 둘러친 난쟁이의 키와
노란색으로 둘러친 난쟁이들 중 안쪽 for문에 의해 현재 탐색되는 난쟁이의 키의 합이,
아홉 난쟁이의 키의 합 - 100과 같을 때,
다시 말하자면, 다음 방정식을 만족할 때

난쟁이들의 키를 저장해둔 리스트에서 탐색을 통해 찾은 가짜 난쟁이들의 인덱스를 따로 저장하고,
탐색을 중단, 즉 2중 for문 모두 벗어나면 됩니다.
탐색을 중단한 후에는,
바로 위에서 저장해둔 가짜 난쟁이들의 인덱스를 이용해,
난쟁이들의 키를 저장해둔 리스트에서 가짜 난쟁이들의 키를 지워주시면 됩니다.
마지막으로, 출력을 위해 난쟁이들의 키를 저장해둔 리스트의 원소를 오름차순으로 정렬하고,
for문을 이용해 리스트의 원소를 차례로 출력해주시면 됩니다.
정리하자면,
1. 변수를 새로 선언하고, 선언한 변수에 난쟁이들의 키를 모두 더한 값을 저장한다.
2. 2중 for문을 이용해 가짜 난쟁이를 다음 방정식을 이용해 판별해낸다.

3. 가짜 난쟁이들의 인덱스를 따로 저장한다.
4. 2중 for문을 벗어난다.
5. 가짜 난쟁이들의 인덱스를 이용해 난쟁이들의 키가 저장된 리스트에서 가짜 난쟁이들의 키를 제거한다.
6. 5의 리스트의 원소들을 오름차순으로 정렬한다.
7. for문을 이용해 리스트의 원소들을 출력한다.
정도가 되겠습니다.
그럼 이제 바로 코드 작성으로 들어가겠습니다.
3. 문제 해결
가장 먼저, 입력부분입니다.
sys.stdin.readline() 함수를 사용하기위해 sys 라이브러리를 불러와주었습니다.
또한, 아홉 난쟁이들의 키를 저장하는 리스트 heights를 선언해줍니다.
마지막으로, sys.stdin.readline() 함수를 이용해 리스트 heights에 난쟁이들의 키를 저장해줍니다.
해당 코드는 다음과 같습니다.
|
1
2
3
4
5
|
import sys
heights = []
for i in range(9):
heights.append(int(sys.stdin.readline()))
|
다음은 2 - 2. 에 정리해둔 알고리즘의 1번 코드입니다.
구현해보면 다음과 같이 간단하게 구현할 수 있습니다.
|
1
|
sum = sum(heights)
|
다음은 알고리즘 2번, 3번, 4번입니다.
2중 for문의 완전 탈출을 위한 bool 타입의 변수 finish를 만들어주고,
가짜 난쟁이들을 찾으면 변수 finish의 값을 True로 해줌으로써, 바깥쪽 for문의 탈출을 조건문을 통해 실행합니다.
또한, 새로운 리스트 save를 만들어 가짜 난쟁이들의 인덱스를 따로 저장해둡니다.
|
1
2
3
4
5
6
7
8
9
10
|
finish = False
for i in range(8):
for j in range(i + 1, 9):
if (heights[i] + heightts[j] == sum - 100):
save = [i, j]
finish = True
break
if (finish):
break
|
다음은 알고리즘 5번입니다.
아래가 해당 코드입니다.
|
1
2
|
del heights[save[0]]
del heights[save[1] - 1]
|
여기서 약간의 실수가 발생할 수 있습니다.
1번째 줄을 실행하게 되면 두 가짜 난쟁이들 중,
리스트의 인덱스 상으로 더 앞에있는, 인덱스가 더 적은 난쟁이가 리스트에서 지워지게 됩니다.
그 이유는 알고리즘 2번, 3번, 4번을 구현한 코드의 2중 for문의 지역변수 i, j 를 보시면 됩니다.
j의 범위는 닫힌 구간 [i + 1, 8] 이기 때문에,
부등식 i < j 가 항상 성립합니다.
또한, save[0] 에는 i의 값이, save[1] 에는 j의 값이 저장되어있기 때문에,
save[0] < save[1] 이 성립하게 됩니다.
이렇게 리스트에서 인덱스 상으로 앞선 난쟁이가 지워지고 나면,
지워지고 남은 리스트의 빈 공간을 채우려 뒤에 있는 원소들이 한 칸씩 앞으로 당겨지게 됩니다.
이때, save[1]의 인덱스를 가지는 가짜 난쟁이도 함께 앞으로 한 칸 옮겨지기 때문에,
정확한 가짜 난쟁이의 인덱스를 찾기 위해서는 save[1]에서 1을 빼줌으로써 정확한 인덱스를 찾아야만 합니다.
다음은 알고리즘 6번입니다.
Python에서는 편리하게 리스트의 원소들을 오름차순으로 정렬해주는 sort() 함수가 있기 때문에,
따로 정렬 알고리즘을 구현하지 않아도 됩니다.
|
1
|
heights.sort()
|
마지막으로 알고리즘 7번, 출력부분입니다.
간단하게 다음과 같이 for문을 이용해 구현할 수 있습니다.
|
1
2
|
for i in heights:
print(i)
|
전체 코드는 다음과 같습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
import sys
heights = []
for i in range(9):
heights.append(int(sys.stdin.readline()))
sum = sum(heights)
finish = False
for i in range(8):
for j in range(i + 1, 9):
if (heights[i] + heights[j] == sum - 100):
save = [i, j]
finish = True
break
if (finish):
break
del heights[save[0]]
del heights[save[1] - 1]
heights.sort()
for i in heights:
print(i)
|
4. 코드 제출 및 결과

해당 코드가 정답임을 확인하실 수 있습니다.
5. 문제의 정답 비율


스페셜 저지 문제여서 그런지, 정답 비율이 절반이 안되는 46.109% 입니다.
6. 다른 정답자들과의 코드 비교
대표적인 정답자분의 코드입니다.
위에서 필자가 2중 for문으로 탐색, 즉 조합(Combination)을 구현했다면,
아래의 정답자분께서는 라이브러리에서 조합 명령어를 불러와 간단하게 해결했습니다.

다만 한 가지 아쉬운 점이 있다면, 4번 째 줄의 매개변수를 7이 아닌 2로 정했다면
시간, 메모리 측면에서 조금 더 이득을 볼 수 있지 않았나하는 생각이 듭니다만,
Python에서는 크게 상관은 없는 부분이기 때문에 주관적으로는 좋은 코드라고 생각합니다.
대표적인 오답자분의 코드입니다.

오답자분이 오답처리 된 이유는, 2중 for문을 완전히 벗어나지 못했기 때문입니다.
16, 17번째 줄을 보시면 2중 for문이지만 break문을 한 번만 걸어줌으로써
안쪽 for문은 탈출하지만, 바깥쪽의 for문은 탈출하지 못하는 코드입니다.
간단한 실수였습니다.
따라서 오답자분께서는 다음과 같이 고침으로써 정답처리를 받을 수 있었습니다.

독자분들께서도 충분히 하실 수 있는 실수이니,
조금 더 유심히 문제 조건과 작성한 코드를 확인할 필요가 있겠습니다.
7. 결론
코드를 짜면서 현재 자신이 생각하고 있는 알고리즘을 추상적인 머리 속이 아닌,
현실의 종이나 화이트보드 같은 곳에 끄적이면서 다시 한번 되짚어 보시는 건 어떤가요?
분명 더 효율적인 알고리즘, 코드들을 작성하실 수 있으실 겁니다.
이번 글은 정말 길어졌습니다...
분량 조절에 실패한 것 같네요.
죄송합니다.
긴 글 읽어주신 여러분들께 진심으로 감사드립니다.
좋은 날 되세요.
'백준 문제집 > Python 배우기(1~50)' 카테고리의 다른 글
| [백준 문제집][Python 배우기 (1~50)][3046] R2(평균) (0) | 2019.12.24 |
|---|---|
| [백준 문제집][Python 배우기 (1~50)][2588] 곱셈(세 자리 곱셈 과정 출력) (0) | 2019.12.23 |
| [백준 문제집][Python 배우기 (1~50)][10430] 나머지 (0) | 2019.12.23 |
| [백준 문제집][Python 배우기 (1~50)][1000, 10998, 1001, 1008, 10869] 사칙연산 (0) | 2019.12.23 |
| [백준 문제집][Python 배우기 (1~50)][2557] Hello World! (0) | 2019.12.23 |




